Navigation of 4-Omini Wheeled using Gradient-based Algorithms and Model Predictive Control
Problem Statement
Consider a simple formulation of rocket landing where the rocket state \(\textbf{x}(t)\) is represented by velocity of the robot \(\dot{x}(t)\), \(\dot{y}(t)\), and angular velocity \(\dot{\theta}(t)\) followed by robot's coordinates \(x(t)\) and \(y(t)\), and orientation \(\theta(t)\), i.e., \(\textbf{x}(t) = [\dot{x}(t), \dot{y}(t), \dot{\theta}(t), x(t), y(t), \theta(t)]^T\), where \(t\) specifies time. The control input \(\textbf{u}(t)\) of the rocket includes angular velocity of each wheel of the robot \(\omega_{1}(t)\), \(\omega_{2}(t)\), \(\omega_{3}(t)\), and \(\omega_{4}(t)\).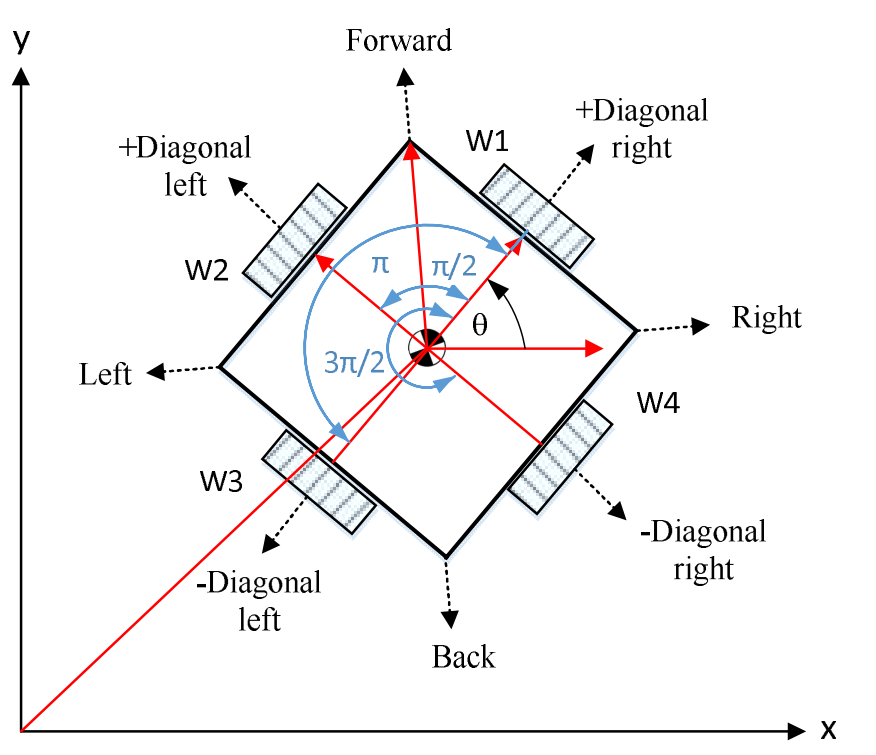
Gradient Based algorithm & Optmization
Problem Statement:
The optimization problem is now formulated as
\[
\begin{aligned}
\min_{w} \quad & \quad ||x(T)||^2 \\
\quad & \quad \dot{x}(t) = \frac{\text{rwheel}}{2}\left(-\sin(\theta+\pi/4)\omega_{1}(t)-\sin(\theta+3\pi/4)\omega_{2}(t)-\sin(\theta+5\pi/4)\omega_{3}(t)-\sin(\theta+7\pi/4)\omega_{4}(t)\right) \\
\quad & \quad \dot{y}(t) = \frac{\text{rwheel}}{2}\left(\cos(\theta+\pi/4)\omega_{1}(t)+\cos(\theta+3\pi/4)\omega_{2}(t)+\cos(\theta+5\pi/4)\omega_{3}(t)+\cos(\theta+7\pi/4)\omega_{4}(t)\right) \\
\quad & \quad \dot{\theta}(t) = \frac{\text{rwheel}}{2}\left( \frac{1}{2\text{rRobot}}\omega_{1}(t)+\frac{1}{2\text{rRobot}}\omega_{2}(t)+\frac{1}{2\text{rRobot}}\omega_{3}(t)+\frac{1}{2\text{rRobot}}\omega_{4}(t)\right), \\
\quad & \quad x(t+1) = x(t) + \dot{x}(t) \Delta t, \\
\quad & \quad y(t+1) = y(t) + \dot{y}(t) \Delta t, \\
\quad & \quad \theta(t+1) = \theta(t) + \dot{\theta}(t) \Delta t \\
\quad & \quad \text{u}(t) = \pi_{w}(\textbf{x}(t)), ~\forall t=1,...,T-1
\end{aligned}
\]
While this problem is constrained, it is easy to see that the objective function can be expressed as a function of \(\textbf{x}(T-1)\) and \(\textbf{u}(T-1)\), where \(\textbf{x}(T-1)\) as a function of \(\textbf{x}(T-2)\) and \(\textbf{u}(T-2)\), and so on. Thus it is essentially an unconstrained problem with respect to \(w\).
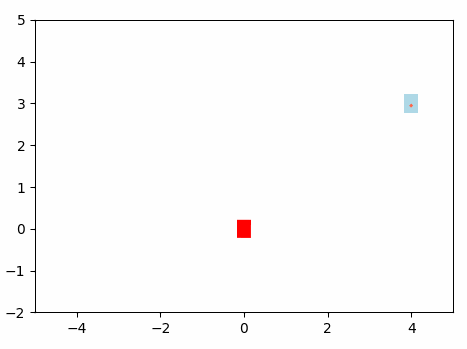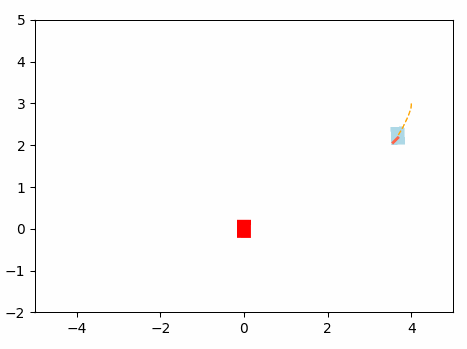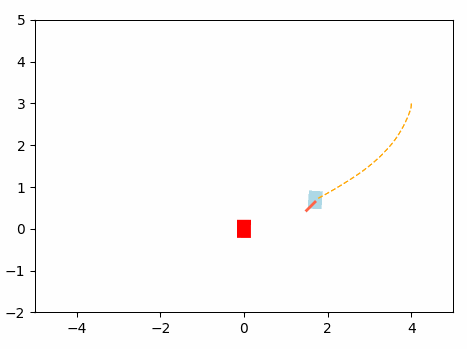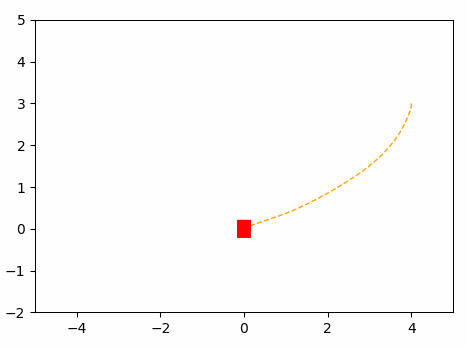
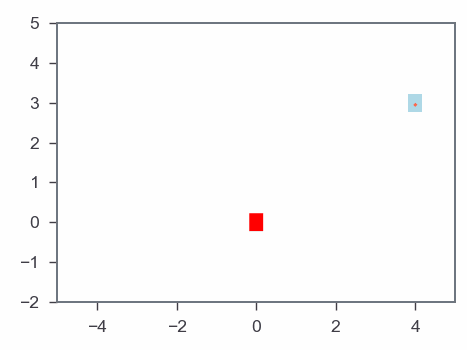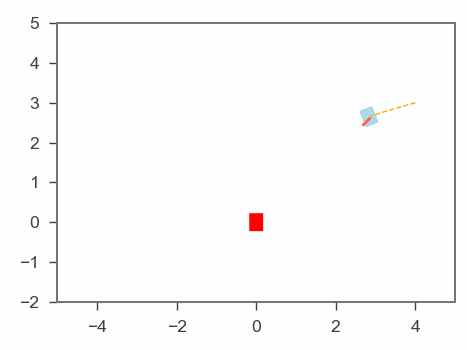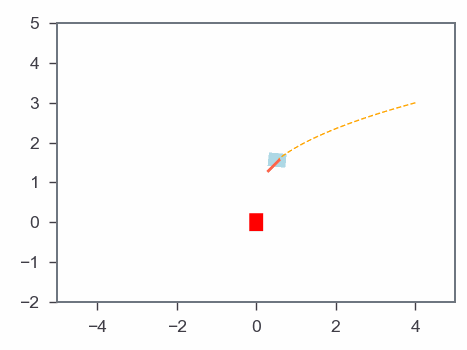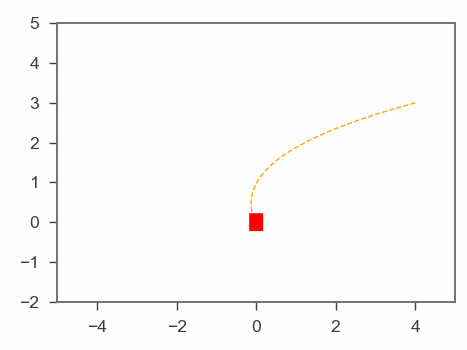
This will be the navigation of the Omini Wheel Controller optimized using Gradient Based Algorithm using Neural Network.
Results: Gradient-based algorithm
MPC & Optmization
Problem Statement:
Using taylor's series, linearized dynamics is passed into MPC algorithm of the dynamics \(f(\textbf{x},u(t))\) at the current state \(\textbf{x}_0\) and zero control input.
\[ A = \nabla_x f = \left[\begin{array}{llll}
1 & 0 & 0 & 0 & 0 & 0\\
0 & 1 & 0 & 0 & 0 & 0\\
0 & 0 & 1 & 0 & 0 & 0\\
\Delta t & 0 & 0 & 1 & 0 & 0\\
0 & \Delta t & 0 & 0 & 1 & 0\\
0 & 0 & \Delta t & 0 & 0 & 1\\
\end{array}\right] \]
and
\[ B = \nabla_u f = \left[\begin{array}{llll}
-\sin(\theta+\pi/4) & -\sin(\theta+3\pi/4) & -\sin(\theta+5\pi/4) & -\sin(\theta+7\pi/4) \\
\cos(\theta+\pi/4) & \cos(\theta+3\pi/4) & \cos(\theta+5\pi/4) & \cos(\theta+7\pi/4) \\
\frac{1}{2*rRobot} & \frac{1}{2*rRobot} & \frac{1}{2*rRobot} & \frac{1}{2*rRobot} \\
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0
\end{array}\right] \]
Then we have
\[ f(\textbf{x},u) \approx f(\textbf{x}_0,0) + A(\textbf{x}-\textbf{x}_0) + Bu \]
\[ f(\textbf{x},u) \approx A\textbf{x} + Bu \]
This will be the navigation of the Omini Wheel Controller optimized using MPC.
Results: MPC Optimization algorithm